Research

My papers on arXiv
My Google Scholar page
My MathSciNet profile

In preparation

• Framed TQFTs from algebra of the infrared
  with Ahsan Z. Khan
    in progress
  
  
• Compatibility of quantum trace map with quantum UV-IR map
  with Samuel Panitch
    in preparation
  
  
• Quivers and BPS states in 3d and 4d
  with Piotr Kucharski, Helder Larraguivel, Pietro Longhi, Dmitry Noshchenko and Piotr Sulkowski
    in preparation
  
  
• Skein traces from curve counting
  with Tobias Ekholm, Pietro Longhi and Vivek Shende
    in preparation
  
  

Papers

1. Knot lattice homology and q-series invariants for plumbed knot complements
   with Rostislav Akhmechet and Peter K. Johnson
     Quantum Topology (2025), published online first [journal | arXiv:2403.14461]
   
   
2. 3d quantum trace map
   with Samuel Panitch
     Algebraic & Geometric Topology (to appear) [arXiv:2403.12850]
   
   
3. Branches, quivers, and ideals for knot complements
   with Tobias Ekholm, Angus Gruen, Sergei Gukov, Piotr Kucharski, Marko Stošić and Piotr Sułkowski
     Journal of Geometry and Physics 177 (2022), 104520 [journal | arXiv:2110.13768]
   
   
4. Inverted state sums, inverted Habiro series, and indefinite theta functions
     preprint [arXiv:2106.03942]
   
   
5. Cobordism invariants from BPS q-series
   with Sergei Gukov and Pavel Putrov
     Annales Henri Poincaré 22 (2021), 4173-4203 [journal | arXiv:2009.11874]
   
   
6. $\hat{Z}$ at large $N$: from curve counts to quantum modularity
   with Tobias Ekholm, Angus Gruen, Sergei Gukov, Piotr Kucharski and Piotr Sułkowski
     Communications in Mathematical Physics 396 (2022), 143-186 [journal | arXiv:2005.13349]
   
   
7. Rozansky-Witten geometry of Coulomb branches and logarithmic knot invariants
   with Sergei Gukov, Po-Shen Hsin, Hiraku Nakajima, Du Pei and Nikita Sopenko
     Journal of Geometry and Physics 168 (2021), 104311 [journal | arXiv:2005.05347]
   
   
8. Large color R-matrix for knot complements and strange identities
     Journal of Knot Theory and Its Ramifications 29 (2020), no. 14, 2050097 [journal | arXiv:2004.02087]
   
   
9. 3d-3d correspondence for mapping tori
   with Sungbong Chun, Sergei Gukov and Nikita Sopenko
     Journal of High Energy Physics 09 (2020), 152 [journal | arXiv:1911.08456]
   
   
10. Higher rank $\hat{Z}$ and $F_K$
      SIGMA 16 (2020), 044, 17 pages [journal | arXiv:1909.13002]
    
    

PhD Thesis

• 3-manifolds, q-series, and topological strings
    Caltech Thesis (2022) [CaltechTHESIS:05252022-010117961]
  
  

  

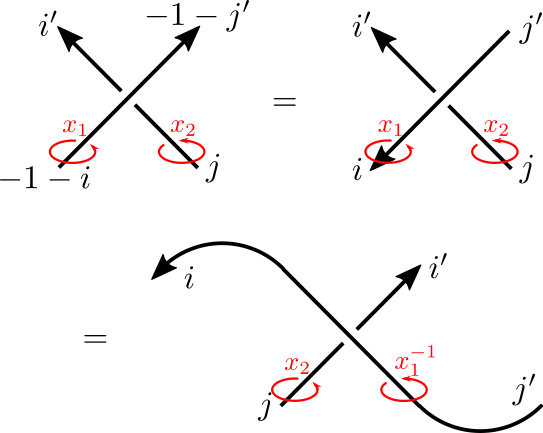
A piece of recreational mathematics

• Prague Clocks
  with Chan Bae, John Conway, Lukas Kohlhase
    The Mathematical Intelligencer 38 (2016), 37 [journal]
  
  

  

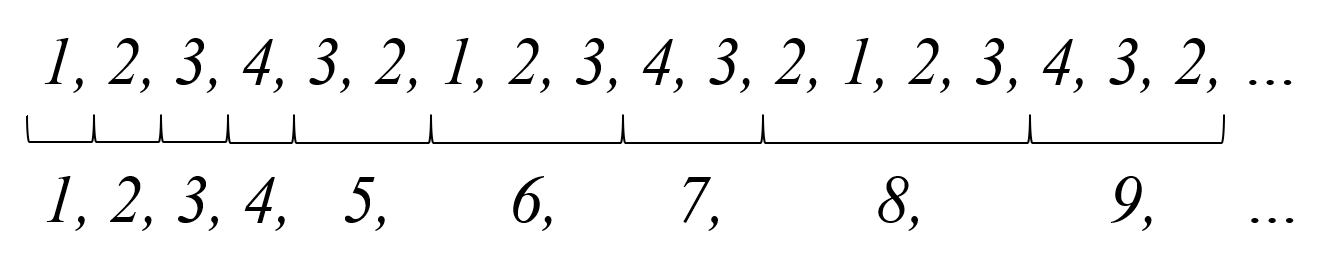
Mathematica files

• Zedhat: a Mathematica package for computation of $\hat{Z}$ for negative definite plumbed 3-manifolds (written by Nikita Sopenko in 2019)
    [Zedhat package | Example usage]
• Large-color R-matrix: computation of $\hat{Z}$ for braid-positive link complements, following arXiv:2004.02087
    [Notebook]
• Inverted state sums: computation of $\hat{Z}$ for braid-homogeneous link complements and more, following arXiv:2106.03942
    [Notebook]